Will you end up with an empty lotería grid?
After a hiatus I’m taking up this week’s FiveThirtyEight Riddler Express which harkens back to a game I played as a child. Each player receives a four-by-four grid of images and a caller randomly draws a card from a deck containing 54 possible images. If a player has that image on their grid, they mark it off and the game ends when one of the players fills their entire card and screams “¡Lotería!”. Each of the 54 possible images can only show up once on each grid. The Riddler asks, what is the probability that a player wipes out and loses without marking off a single image on his or her grid. And how does that probability change based on the size of the grid and the number of images?
Calculating the probability
The probability we are seeking boils down to the probability that none of the images on your grid are also on your opponent’s grid. If we number all images from 1 to 54, then, without loss of generality, if your opponent’s grid includes images numbered 1-16, then all of the images on your grid should be in the range of 17-54. Accordingly, the probability that the image on your first square is not on your opponent’s grid is:
\[ \frac{54-16}{54} \] Since images are not repeated on a given grid, the probability that the next image is also not on your opponent’s grid is:
\[ \frac{53-16}{53} \] and so on.
The probability that none of your 16 images are also on you opponents’ grid is: \[ \prod_{i=0}^{i=15} \frac{54-i-16}{54-i} \]
Which is quite unlikely as we can see from this line of R code:
library(tidyverse)
0:15 %>% map_dbl(~ (54 -.x -16) / (54 - .x)) %>% prod()[1] 0.001054281
Different sized grids and number of images
Below we explore how grids of ranging from 2x2 to 7x7, as well as 20-70 images change the probability of wiping out. As shown, the larger the grid and the more images there are, the less likely that a player doesn’t mark off a single image becomes. The cases on the lower right are not valid since there are fewer images than squares on the grid.
loteria <- function(grid=16, symbols=54) {
seq(from=0, to=(grid-1)) %>%
map_dbl(~ (symbols -.x -grid) / (symbols - .x)) %>% prod()
}
gridprob <- data.frame(x=rep(c(4,9,16,25,36,49),6),
y=rep(c(20,30,40,54,60,70), each=6))
gridprob$Prob <- map2_dbl(gridprob$x, gridprob$y, loteria)
ggplot(gridprob, aes(x=as.factor(x),y=as.factor(y),fill=Prob)) +
geom_tile(color='white') +theme_bw(base_size = 15) +
scale_fill_viridis_c(option = 'D') +coord_fixed() +
labs(x='Grid size', y='Number of images', caption='By @cortinah; May 31, 2019',
title='¡Lotería! Riddler Express',
subtitle = 'Probability of one player losing with empty grid')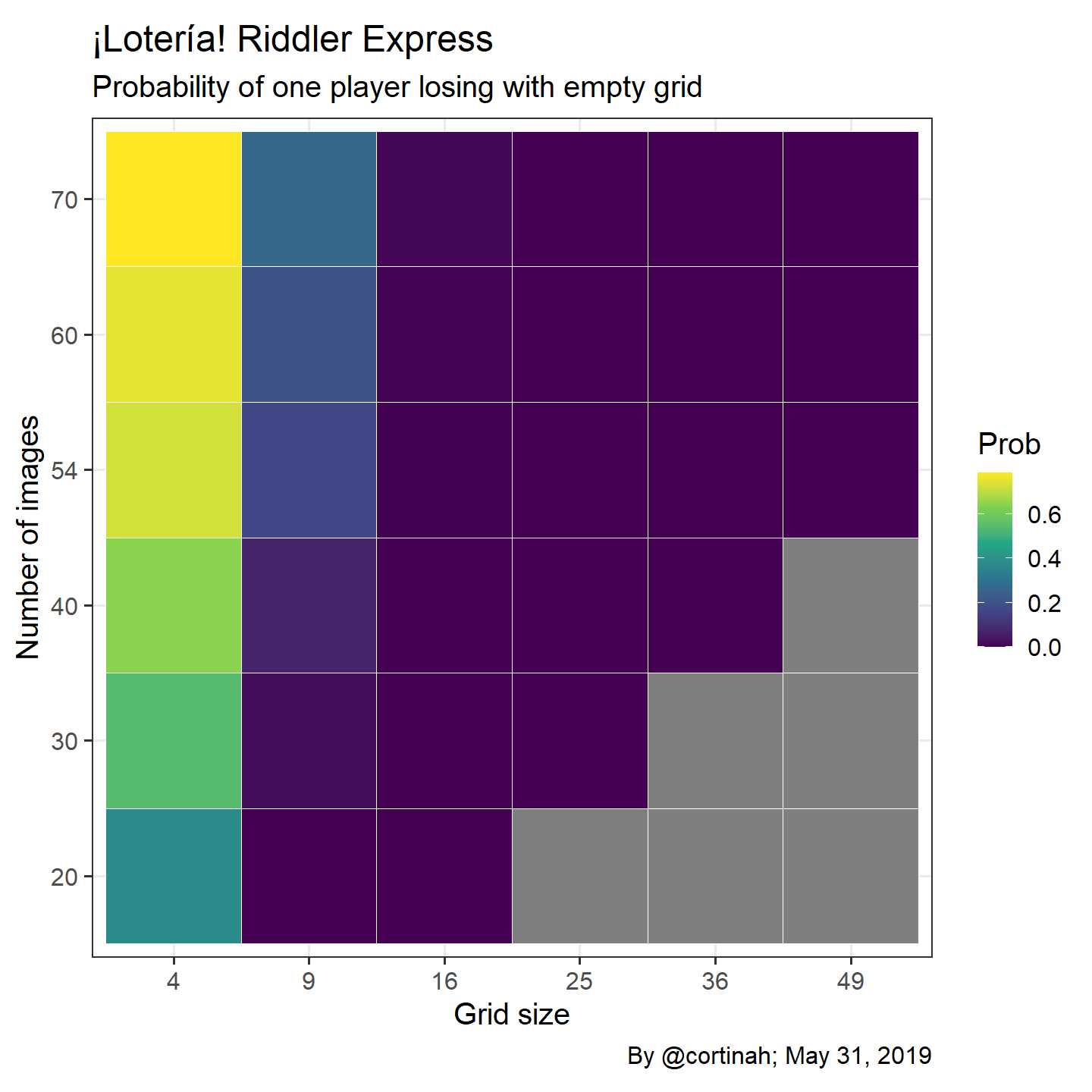
¡Gracias Señor Ollie!