Can you fool the bank with your counterfeit bills?
In this week’s FiveThirtyEight Riddler Express you are a counter
How many fake notes should you add to the $2,500 in order to maximize the expected value of your bank account? How much free money are you likely to make from your strategy?
The odds of getting caught
We ignore for a moment to gain some intuition about the problem the issue of rounding up to the nearest whole. The probability of any given fake bill being discovered is $ 0.05 \cdot 0.25 = 0.0125 $. The probability of not getting caught is hence $ 1 - 0.0125 = 0.9875 $. If you deposit $ f $ forged bills, then the probability of not being caught is $ 0.9875 ^ {f} $. The expected value of attempting to deposit $ f $ forged bills and 25 real ones is:
\[ E(f) = 100 \cdot (f + 25) \cdot 0.9875^{f} \]
Below is what the function looks like. It increases initially as more fakes are added, peaking around 50-55, then decreases as the growing probability of being caught outweighs the benefit of adding more fake bills.
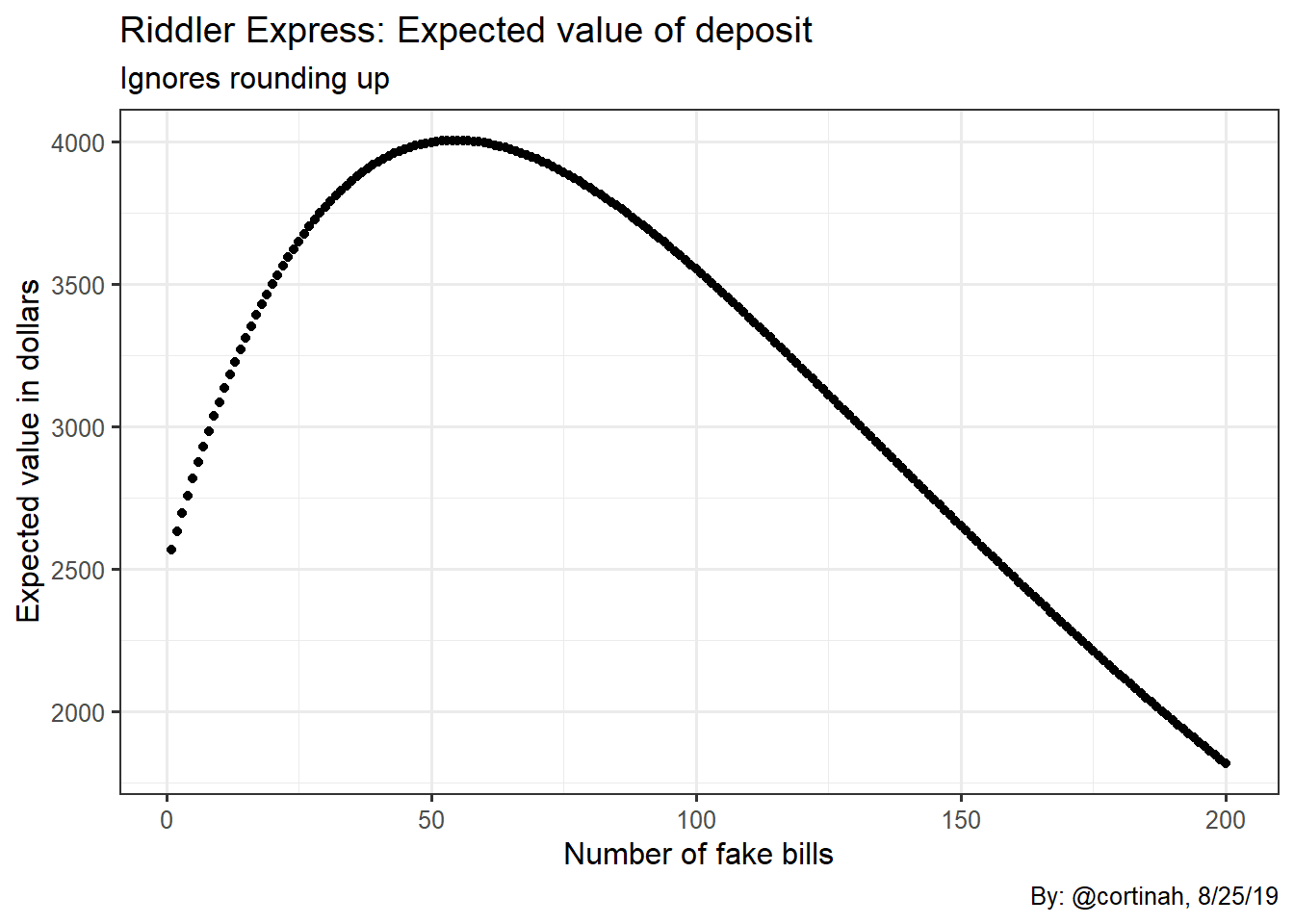
The optimal maximum number of fake bills is 54, with a net profit of $5,400.
money <- function(x) 100*(x+25)*(0.9875^x)
which(map_dbl(1:100, money) == max(map_dbl(1:100, money)))[1] 54
Incorporating the bank’s “rounding up” checks
In the puzzle statement the bank’s approach is to round up the number of bills it examines according to its 5% procedure. We now incorporate this constraint as shown below. The expected value now becomes:
\[ E(f) = 100 \cdot (f + 25) \cdot ( 1- \frac{ceiling(f \cdot 0.05)}{f} \cdot 0.25)^{f} \]
The plot is now discontinuous, as the rounding up causes more bills to be examined, resulting in greater probabilities of being caught than before (except on multiples of 20 fakes), and therefore lower expected values.
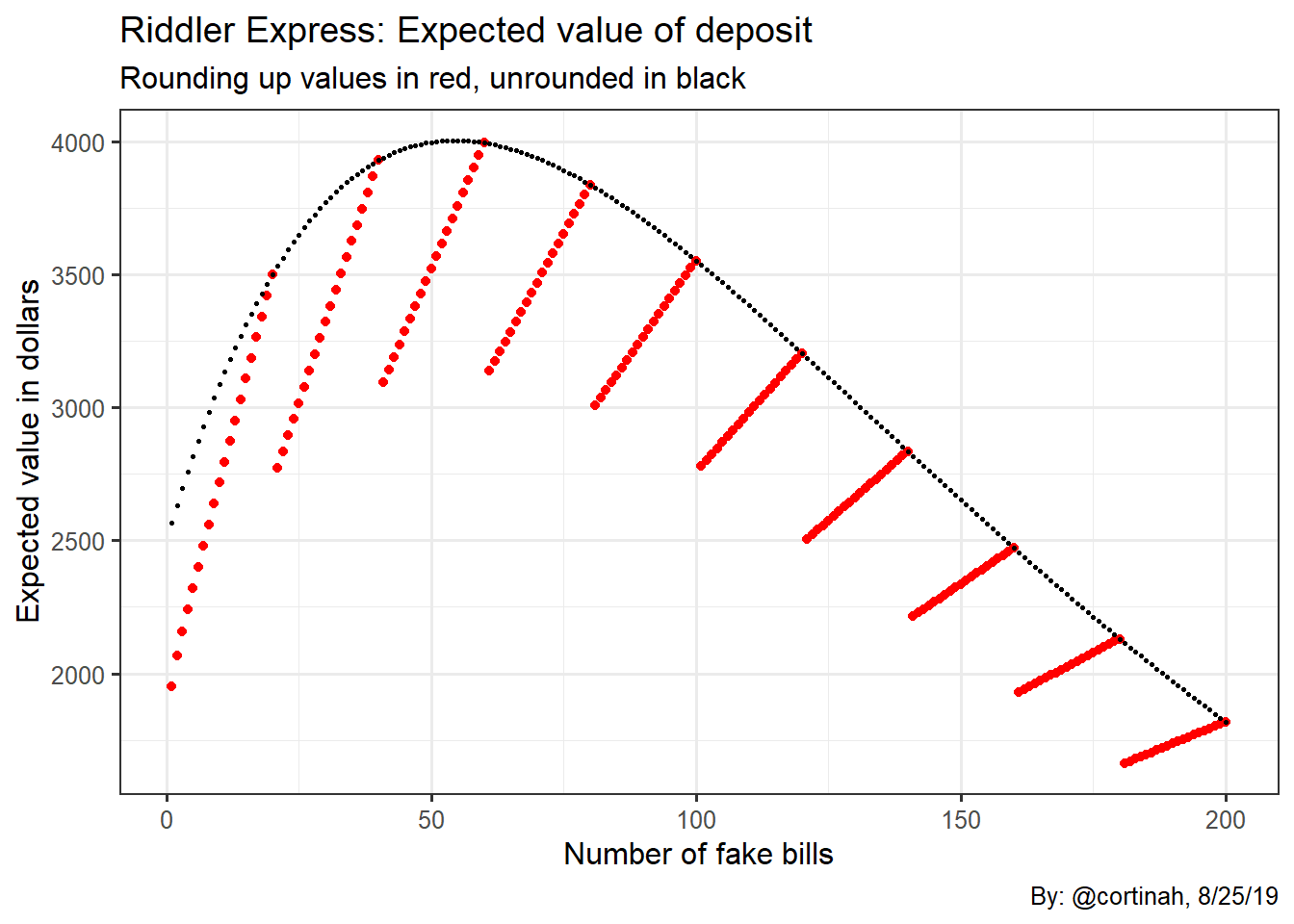
The new optimal value of fakes is 60, with a corresponding net profit of $6,000
money <- function(x) 100*(x+25)*((1-ceiling(x*0.05)/x*0.25))^x
which(map_dbl(1:100, money) == max(map_dbl(1:100, money)))[1] 60
Why is the optimum higher with the rounding up constraint?
It may appear surprising at first that the rounding up constraint, which entails more bills being subject to examination, results in a higher optimal value of fakes. However, as we can see in the above chart the black dots are always above or at the same level as the red dots. This means that even with a higher optimal of 60, the expected value with the rounding constraint and 60 fakes is $3,996 which is below the expected value without the rounding constraint and 54 fakes of $4,005. The rounding up constraint does indeed make the forgery business a little less attractive for the forger.
A fun puzzle as always Ollie. Thank you.